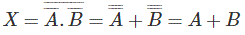▷ Puerta NAND ◁

Published by Rommer Seo viernes, 6 de diciembre de 2019

Cuando la salida de una compuerta AND se invierte a través de una compuerta NOT, la operación se llama operación NAND. La puerta lógica que realiza esta operación NAND se llama puerta NAND.

Una puerta NOT seguida de una puerta AND hace una puerta NAND . La construcción lógica básica de la puerta NAND se muestra a continuación,


El símbolo de la puerta NAND es similar a la puerta AND, pero se dibuja una burbuja en el punto de salida de la puerta AND, en el caso de la puerta NAND. El símbolo de la puerta NAND se muestra a continuación.

La compuerta NAND significa "no compuerta AND", lo que significa que la salida de esta compuerta es exactamente inversa a la de una compuerta AND similar. Sabemos que la salida de la compuerta AND es alta o 1 cuando todas las entradas son altas o 1. En todos los demás casos, la salida de la compuerta AND es baja o 0. En la NAND, el hecho es lo contrario, aquí, la salida es solo 0 lógico cuando y solo cuando todas las entradas de la puerta son 1s, y en todos los demás casos, la salida de la puerta NAND es alta o 1.
Por lo tanto, la tabla de verdad de una puerta NAND se puede escribir como,

Justo al revés de la tabla de verdad de la puerta AND que es

Al igual que la compuerta AND, una compuerta NAND también puede tener más de dos entradas, como 3, 4, compuerta NAND de entrada.
Una puerta NAND también se conoce como puerta lógica universal, ya que todas las operaciones binarias se pueden realizar utilizando solo puertas NAND.
Hay tres operaciones binarias básicas, AND, OR y NOT. Mediante estas tres operaciones básicas, uno puede realizar todas las operaciones binarias complejas. Ahora, mostraremos cómo podemos lograr estas tres operaciones binarias usando solo compuertas NAND.

Darse cuenta de la puerta NO utilizando la puerta NAND

Cuando ambas entradas de una compuerta NAND de dos entradas son cero, la salida es 1, y ambas entradas de la compuerta NAND son 1, la salida es 0. Por lo tanto, una compuerta NOT puede realizarse fácilmente desde compuertas NAND simplemente aplicando entradas comunes a la puerta NAND o cortocircuito todos los terminales de entrada de una puerta NAND.

Donde, X es 1 o 0.

Realizando AND Gate usando NAND Gate

Como dijimos anteriormente, una puerta NAND es una puerta NOT seguida de una puerta AND, por lo que si podemos cancelar el efecto de la puerta NOT en una puerta NAND, se convertirá en una puerta AND. Por lo tanto, una puerta NOT seguida de una puerta NAND realiza una puerta AND. En este caso, usamos las compuertas NOT realizadas a partir de compuertas NAND, y mostramos el circuito lógico a continuación, 

Realizando la puerta OR desde la puerta NAND

Por el teorema de De Morgan sabemos

La ecuación anterior es una operación OR lógica.

La ecuación lógica anterior se puede representar mediante puertas como se muestra arriba, donde las entradas primero se invierten y luego pasan a través de una tercera puerta NAND.
La tabla de verdad de tal circuito es,

Ahora, hemos demostrado que las tres operaciones binarias básicas se pueden realizar utilizando solo compuertas NAND. Por lo tanto, cualquier otra operación binaria simple o compleja también debe realizarse utilizando solo puertas NAND y, por lo tanto, está justificado llamar a las puertas NAND como puertas universales.